t-test pre nezávislé výbery (nepárový t-test)

Pojem, predpoklady. t-test pre nezávislé výbery je všeobecne používaná metóda na vyhodnotenie rozdielu v priemeroch dvoch skupín. Nap., t-test môže byť použitý na vyhodnotenie rozdielu v testovanej veličine medzi experimentálnou skupinou pacientov užívajúcich liek, a kontrolnou skupinou, ktorá obdržala iba placebo. Teoreticky je t-test možné použiť aj vo veľmi malých vzorkách (n=10, niektorí výskumníci tvrdia, že dokonca aj v menších), ak však je dodržaný predpoklad normálneho rozloženia v oboch skupinách, a rozptyly týchto skupín sa významne nelíšia. Normalita môže byť odhadnutá z histogramu, alebo vykonaním testu normality. Predpoklad zhodnosti rozptylu verifikujeme F testom, alebo použijeme robustnejšiu techniku, Levenov test. Ak tieto predpoklady nie sú splnené, použijeme neparametrickú alternatívu t-testu Mann-Whitneyov U test alebo Kolmogorov-Smirnov test.

p-hodnota, ktorá je vypočítaná t-testom reprezentuje pravdepodobnosť chyby vyvolanej akceptovaním výskumníkovej hypotézy o existencii rozdielu medzi skúmanými skupinami. Technicky povedané, je to pravdepodobnosť chyby, že zamietneme nulovú hypotézu o neexistencii rozdielu medzi skupinami, ak táto naozaj platí. Ak sa smer rozdielu dá predvídať, môžme získanú p-hodnotu podeliť dvoma. (namiesto obojstrannej alternatívnej hypotézy "priemery sa nerovnajú" - two tailed probability- máme jednostrannú, "prvý je menší (resp. väčší) ako druhý"-one tailed probability).

Usporiadanie dát. Na vykonanie t-testu pre nezávislé výbery potrebujeme jednu nezávisle premennú, spravidla alternatívneho typu, takzvanú grupujúcu premennú (napr. pohlavie: muž/žena) a aspoň jednu závisle premennú (nejaké testované skóre), intervalového typu. Budú porovnané priemery závisle premennej medzi vybranými skupinami založenými na vybratých hodnotách nezávislej premennej. Na nasledujúcich dátach bude prevedený t-test porovnávajúci priemer WCC skóre mužov a žien. Zistený rozdiel medzi skupinami sa dá chápať aj ako závislosť týchto dvoch premenných.

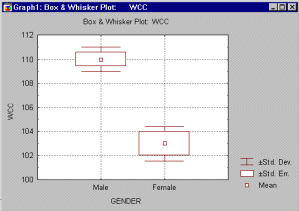
t-test a grafy. V analýze t-test môže byť porovnanie dvoch priemerov a miery rozptylu v dvoch skupinách vizualizované v takzvanom krabicovom grafe (box and whisker plot). Tento graf umožňuje okamžite odhadnúť silu relácie medzi grupujúcou a závisle premennou.

Komplexnejšie skupinové porovnania. Často sa stáva, že je treba porovnať viac ako dve skupiny v jednej grupujúcej premennej (napr. typ lieku: liek1, liek2, placebo), alebo členiť závisle premennú podľa viacerých grupujúcich (napr. podľa pohlavia aj typu lieku). Vtedy môžme použiť analýzu rozptylu, ktorá sa dá považovať za zovšeobecnenie t-testu. Pre porovnanie dvoch skupín dáva identický výsledok ako t-test, pre komplexnejšie skupinové porovnania ponúka ďalšie výhody oproti sérii t-testov vykonanej pre všetky možné dvojice skupín.

Rozptyl vo vnútri skupiny. Veľkosť relácie medzi dvoma premennými, takisto aj rozdiel priemerov dvoch skupín závisí od veľkosti rozptylu vo vnútri každej skupiny. Napr., ak prvý priemer je 50 a druhý 52, pričom hodnoty prvej premennej kolíšu od 49 do 51 a druhej od 51 do 53, tak rozdiel 2 medzi priemermi bude významný. Ale ak hodnoty prvej aj druhej premennej sú široko rozptýlené od 0 do 100, tak rozdiel 2 je zanedbateľný.Z toho vyplýva, že čím menší je rozptyl vo vnútri skupín, tým je t-test citlivejší.

Preložené z:
StatSoft, Inc. (1999). Electronic Statistics Textbook. Tulsa, OK: StatSoft. WEB: http://www.statsoft.com/textbook/stathome.html