t-test pre závislé výbery (párový t-test) - príklad v programe STATISTICA

STATISTICA - modul Basic statistics and tables.

Daný je dátový súbor Dipl.sta, 64 stĺpcov (variables) X 159 riadkov (cases), v ktorom sú údaje o mačacích kostrách. Dĺžka pravej polovice sánky - DLZ_S_P, dĺžka ľavej polovice sánky - DLZ_S_L, výška mačky - VYSKA, obvod hlavy - hlava,...

Predmetom záujmu budú premenné DLZ_S_P a DLZ_S_L. V prvom rade je treba urobiť popisnú štatistiku z rozdielu premenných v Analysis/Descriptive statistics s cieľom overiť predpoklad normality u oboch výberov.
Cieľom t-testu je zistiť, či existuje významný rozdiel medzi priemernou dĺžkou pravej a ľavej polovice sánky, teda existencia asymetrie v danej, napr. zamorenej lokalite. Zvolíme Analysis/t-test for dependent samples a vyplníme dialógové okno:

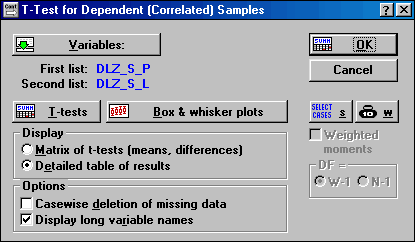
V tomto prípade boli zvolené vo variables premenné DLZ_S_P a DLZ_S_L, v sekcii display detailný spôsob výstupu, a v sekcii options aj zobrazovanie dlhých názvov premenných. Ak v sekcii options nie je zaškrtnuté "casewise deletion of missing data", mažú sa chýbajúce merania po pároch. Výsledok je:

Vo výstupe sú priemery a štandardné odchýlky oboch výberov, počet respondentov, rozdiel priemerov, štandardná odchýlka výberu vytvoreného z rozdielov párových hodnôt, hodnota testovacej štatistiky t, počet stupňov voľnosti a hodnota p. Ak je hodnota p<0,05 (aj červená farba) znamená to významnosť. Tento prípad v tomto príklade nenastal, takže nezamietame nulovú hypotézu o tom, že priemerná dĺžka ľavej a pravej polovice sánky celej populácie mačiek v danej lokalite sú zhodné.
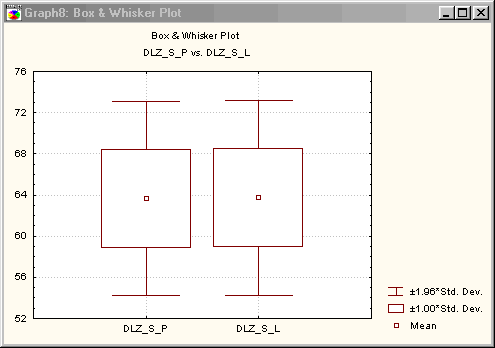
Všimnime si, že vo vstupnom dialógovom okne sú ešte možnosti pre grafickú prezentáciu. To isté sa dá nájsť aj v popisnej štatistike. Na ilustráciu bol vybratý krabicový graf, jedna z jeho štyroch možných podôb.